1. 分类问题

区别于CS229 note 1: Introduction提到的回归问题，我们这里要研究的问题是分类，即输出变量是离散的，非黑即白、非一即二，取值范围不再是实数。

对于2-分类问题，我们倾向于找到一个函数h(x)，输入特征x后，给出0或者1的结果。看起来就是一个简化版的回归问题，毕竟结果不需要精确到数字，只需要给出一个类别就可以了。可不可以利用回归问题的解决思路来解决分类问题？答案是也可以，但会出现一系列的问题，相当于用一个复杂的模型去拟合一个简单的数据。

直观来讲，我们只需要设置某个阈值，高于此阈值的为1，低于此阈值的为0即可。没错，这是一种分类方法。

$$g(z)=\left\{\begin{array}{ll}{1} & {\text { if } z \geq 0} \\ {0} & {\text { if } z<0}\end{array}\right.$$

还有其他的分类方法，比如Sigmoid函数，该函数具有良好的性质，比如光滑可求导，值域在(0,1)内等等。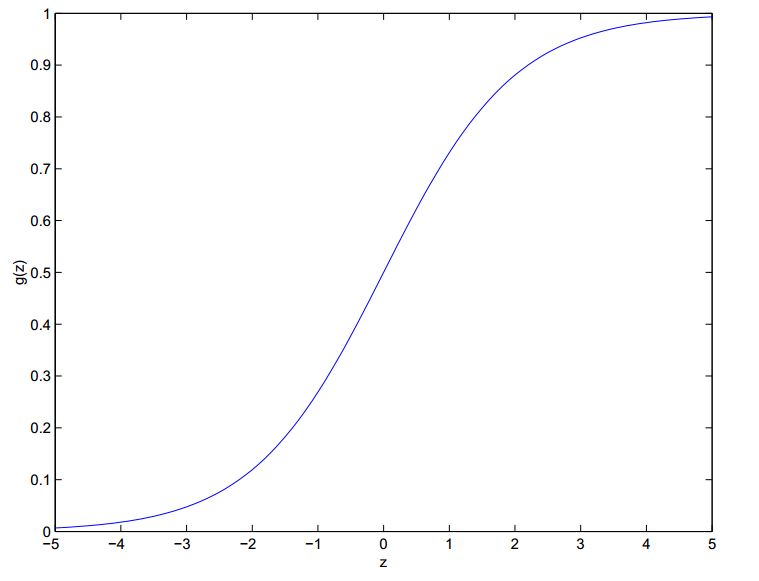

$$g(z)=\frac{1}{1+e^{-z}}$$

我们利用Sigmoid函数作为$h_{\theta}(x)$，调整θ，使得分类器效果最好，这就是逻辑斯蒂回归模型。

$$h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}$$

请注意，虽然是回归模型，但逻辑斯蒂回归做的事情其实是分类。问题又切换到如何构建一个合理的、以θ为变量的函数，对其优化、找到最低点？

让我们以抛硬币为例，阐述二元分类问题。抛硬币事件符合0-1分布，即事情发生是1，不发生是0。如果连续抛很多次硬币，问有多少次正面，多少次反面的概率，那这就是伯努利分布，即二项分布。

二分类问题也是如此，已知样本x，在参数为θ的情况下，y=1即正面的概率，即为h(x)，y=0即反面的概率为1-h(x)。

$$\begin{array}{l}{P(y=1 | x ; \theta)=h_{\theta}(x)} \\ {P(y=0 | x ; \theta)=1-h_{\theta}(x)}\end{array}$$

将两个式子通过一些数学技巧结合起来，方便数学讨论：

$$p(y | x ; \theta)=\left(h_{\theta}(x)\right)^{y}\left(1-h_{\theta}(x)\right)^{1-y}$$

推广到全部数据：在参数为θ时，已知输入数据集为X，则输出为$\vec y$的概率可以用下面的函数来表示：

$$\begin{aligned} L(\theta) &=p(\vec{y} | X ; \theta) \\ &=\prod_{i=1}^{m} p\left(y^{(i)} | x^{(i)} ; \theta\right) \\ &=\prod_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)\right)^{y^{(i)}}\left(1-h_{\theta}\left(x^{(i)}\right)\right)^{1-y^{(i)}} \end{aligned}\\ \begin{aligned} \ell(\theta) &=\log L(\theta) \\ &=\sum_{i=1}^{m} y^{(i)} \log h\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h\left(x^{(i)}\right)\right) \end{aligned}$$

又变成了我们熟悉的最大似然估计问题，即求θ，使得$\ell(\theta)$最大。我们既可以求导数，也可以采用随机梯度下降法。

$$\begin{aligned} \frac{\partial}{\partial \theta_{j}} \ell(\theta) &=\left(y \frac{1}{g\left(\theta^{T} x\right)}-(1-y) \frac{1}{1-g\left(\theta^{T} x\right)}\right) \frac{\partial}{\partial \theta_{j}} g\left(\theta^{T} x\right) \\ &=\left(y \frac{1}{g\left(\theta^{T} x\right)}-(1-y) \frac{1}{1-g\left(\theta^{T} x\right)}\right) g\left(\theta^{T} x\right)\left(1-g\left(\theta^{T} x\right)\frac{\partial}{\partial \theta_{j}} \theta^{T} x\right.\\ &=\left(y\left(1-g\left(\theta^{T} x\right)\right)-(1-y) g\left(\theta^{T} x\right)\right) x_{j} \\ &=\left(y-h_{\theta}(x)\right) x_{j} \end{aligned} \\ \begin{aligned}\theta_{j} :=\theta_{j}+\alpha\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)}\end{aligned}$$

有没有感觉求偏导数后的形式与回归问题很相似？这背后又有着怎样的共同点？

还有更巧的呢。记得我们之前说的$
g(z)=\left{\begin{array}{ll}{1} & {\text { if } z \geq 0} \ {0} & {\text { if } z<0}\end{array}\right.
$吗？采用该分类函数作为分类器进行训练的模型，叫做感知器(perceptron learning algorithm)模型。它的梯度下降算法也是这种形式：$\theta{j} :=\theta{j}+\alpha\left(y^{(i)}-h{\theta}\left(x^{(i)}\right)\right) x{j}^{(i)}$

这背后的原因将留在我之后的更新中解答。

2.其他优化似然函数的方法：牛顿法

除了前面说的梯度下降法，牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法遵循这样的优化规则：

$$\theta :=\theta-\frac{f(\theta)}{f^{\prime}(\theta)}$$

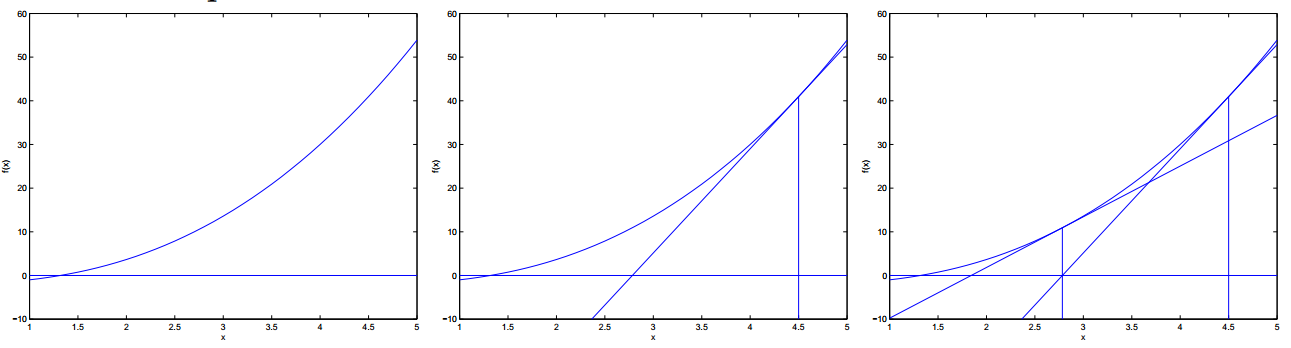
首先选择一点，从该点作函数的切线，交x轴于新的点x2，x2再作切线，交x轴于新的点x3，如上图所示。

最终牛顿法会找到f(x)最小时的x值，整个过程会很快，比梯度下降要快。
如果我们想要优化的函数是$\ell^{\prime}(\theta)$，则牛顿法优化规则为：

$$\theta :=\theta-\frac{\ell^{\prime}(\theta)}{\ell^{\prime \prime}(\theta)}$$

上面我们假设θ是一个实变量。如果θ是一个向量，则牛顿法变成：

$$\theta :=\theta-H^{-1} \nabla_{\theta} \ell(\theta)$$

其中：

$$H_{i j}=\frac{\partial^{2} \ell(\theta)}{\partial \theta_{i} \partial \theta_{j}}$$

像这样将牛顿法应用于逻辑斯蒂回归的似然函数优化问题上，叫做fisher’s scoring。

3. 总结

我们主要讨论了分类问题的概念，二分类问题的处理方法：感知器、逻辑斯蒂回归，以及将牛顿法应用于逻辑回归。